Removing What Seam Carving Found

Background

Seam carving [2] is an algorithm for content-aware image resizing. It functions by searching for a number of seams (paths of least importance) in an image and removing these seams to reduce image size. The basic idea can be demonstrated with the following images from Wikipedia:

Seam carving searches for seams which are indicated by red lines:

After removing these seams, we get the resulting image:

The original algorithm [1] finds one seam each time. To shrink an image to a specific size, we first shrink the image in the vertical direction by multiple search and removing operations to get an intermediate image. Then we do the same on the intermediate image horizontally.

vertical:       search -> remove -> search -> remove -> ...
horizontal:     search -> remove -> search -> remove -> ...

This is too slow for large images, thus an algorithm [3] was proposed, which can find multiple seams of one direction in one pass. We could shrink an image by calling this algorithm two times.

vertical:       search -> remove
horizontal:     search -> remove

In one of our systems using [3], we tried to reduce the number of removing operations to one by searching two times to find seams in both directions and remove them all at a time.

vertical:       search
horizontal:     search
two directions: remove

Intuitively, it’s as easy as removing seams in one direction, but our practice shows it’s not. This text explains the reason.

The Intuitive Algorithm

If there are only vertical or horizontal seams, removing them is simple. Taking the vertical case as an example, for any pixel (i, j) in the input image, where i is the row index, j is the column index, it will be mapped to the pixel (i, j - co(i, j)) in the resulting image, where co(i, j) is the number of vertical seams on the left of the pixel (i, j) in the input image. Denoting the input image as x, the resulting image as y, and indexes starting from 0, we have:

y[i][j - co(i, j)] = x[i][j]

, for i in [0, x.height), j in [0, x.width), and x[i][j] is not passed through by any seam.

Similarly, if there are only horizontal seams, we have:

y[i - ro(i, j)][j] = x[i][j]

, for i in [0, x.height), j in [0, x.width), and x[i][j] is not passed through by any seam. Here ro(i, j) is the number of horizontal seams above the pixel (i, j) in x.

Combining two cases, for both vertical and horizontal seams, we have:

y[i - ro(i, j)][j - co(i, j)] = x[i][j]

, for i in [0, x.height), j in [0, x.width), and x[i][j] is not passed through by any seam.

However, this algorithm is not correct for two reasons. The first reason is that multiple pixels in x may be mapped to the same pixel in y. The second reason is that some positions in y may not be mapped by any pixel in x.

Duplicated Mapping

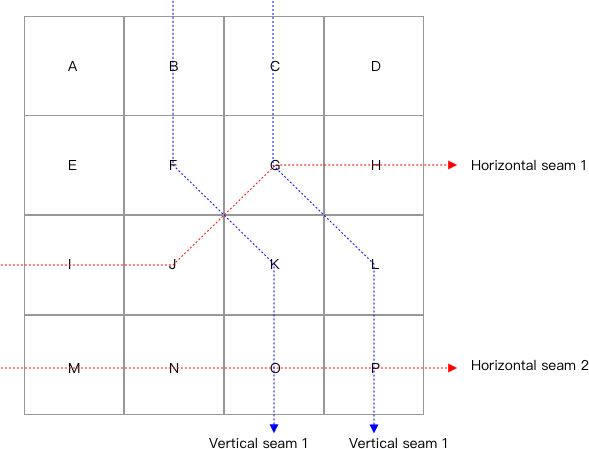
The example is a 4x4 image. To very microscopically observe it, we draw it as the following grids. Each grid represents a pixel of the image, and we draw seams on it, blue for the vertical, red for the horizontal. As the grids show, two pixels of the input image can be mapped to the same position. For pixel M(3, 0), there’re 2 horizontal seams above it and no vertical seams on the left of it, so we have ro[3][0] = 2 and co[3][0] = 0, thus it will be mapped to (1, 0) in the resulting image. For pixel K(2, 2), we have co[2][2] = 2 and ro[2][2] = 1, thus it will also be mapped to (1, 0).

Lack of Mapping

Again, we take a 4x4 image presented in the following grids as an example. We label every pixel with letters and draw seams on it, blue for the vertical, red for the horizontal. Observe that every pixels right to or below F(1, 1) is removed by seams, so no pixel will be mapped to (1, 1).

Drawing the resulting image will make this more clear:

We can see that the result can not even form a rectangle.

Remarks

Why does intuition fail on such simple task? When we think about an image, the brain regards it as an continuous object but the image is actually discrete pixels. The mental model mismatches and one-byte-off errors arise.

References