LNN: A Command-Line Program of Feedforward Neural Networks

LNN (Little Neural Network) is a command-line program training and running feedforward neural networks. LNN aims to make easy tasks easily done. This report contains a user’s guide and several examples to explain the design of LNN.

This report describes the first version (0.0.1) of LNN. Like many programs, LNN evolves. There may be some new features of later versions not contained by this report.

The code of LNN is hosted at GitHub https://github.com/dongyx/lnn.

Table of Contents

• 1. Introduction
• 2. Learning Addition of Real Numbers
• 3. Recognizing Hand-Written Digits
• 4. Recognizing Spam SMS Texts
• 5. Remarks
• Appendix 1. Training Options
• Appendix 2. Loss Functions
• Appendix 3. Activation Functions
• Appendix 4. MNIST Utilities
• Appendix 5. SMS Spam Utilities
• References

---

1. Introduction

The following call of LNN creates a network with a 10-dimension input layer, a 5-dimension hidden layer with the sigmoid activation function, and a 3-dimension output layer with the softmax activation function.

$ lnn train -C q10i5s3m samples.txt >model.nn

The -C option creates a new model with the structure specified by the argument. The argument here is q10i5s3m. The first character q specifies the loss function to be the quadratic error. The following three strings 10i, 5s, 3m represent that there are 3 layers, including the input layer, with dimensions 10, 5, 3, respectively. The character following each dimension specifies the activation function for that layer. Here i, s, and m represent the identity function, the sigmoid function, and the softmax function, respectively (Appendix 2, 3).

In the remaining part of this chapter, the dimension of input is denoted by \(n\), and the dimension of output is denoted by \(m\).

LNN reads samples from the file operand, or, by default, the standard input. The trained model is printed to the standard output in a text format.

The sample file is a text file containing numbers separated by white characters (space, tab, newline). Each \(n+m\) numbers constitute a sample. The first \(n\) numbers of a sample constitute the input vector, and the remaining constitute the output vector.

LNN supports many training arguments like learning rate, iteration count, and batch size. The complete list is documented in Appendix 1.

LNN could train a network based on an existed model by replacing -C with -m.

$ lnn train -m model.nn samples.txt >model2.nn

This allows one to observe the behaviors of the model in different stages and provide different training arguments (Chapter 4).

The run sub-command runs an existed model.

$ lnn run -m model.nn input.txt

LNN reads the input vectors from the file operand, or, by default, the standard input. The input shall contain numbers separated by white characters (space, tab, newline). Each \(n\) numbers constitute an input vector.

The output vector of each input vector is printed to the standard output. Each line contains an output vector. Components of an output vector are separated by a space.

The test sub-command evaluates an existed model.

$ lnn test -m model.nn samples.txt

LNN reads samples from the file operand, or, by default, the standard input. The mean loss value of the samples is printed to the standard output. The format of the input file is the same as of the train sub-command.

2. Learning Addition of Real Numbers

This chapter trains a network to add two numbers with LNN. The training could be done with a single Shell statement.

$ seq 1024 \
| awk 'BEGIN {srand(1)} {x=rand(); y=rand(); print x,y,x+y}' \
| lnn train -Cq2i1i -i1024 >model.nn

The seq | awk part generates 1024 samples whose addends are between 0 and 1. These samples are then piped to LNN. The trained model is redirected to the file model.nn. The argument q2i1i means a 2-dimension input layer, a 1-dimension output layer, and the quadratic error loss function, no activation functions. The -i option sets the iteration count to be 1024.

Evaluating the model is also very simple. The following call shows that the loss on the test set is 0.

$ seq 1024 \
| awk 'BEGIN {srand(2)} {x=rand(); y=rand(); print x,y,x+y}' \
| lnn test -mmodel.nn

0.000000

The test script is similar with the training script except that

• The random seed is different to avoid the test set from being the same with the training set;
• The train sub-command of LNN is replaced with the test sub-command.

This model could be used as an addition calculator.

$ echo 231 -100 | lnn run -m model.nn
131.000000

3. Recognizing Hand-Written Digits

The MNIST database of handwritten digits [2], has a training set of 60000 examples, and a test set of 10000 examples. Each sample is a 28x28 gray-scale image (784 pixels) labeled by 0~9. This chapter uses the MNIST database to train a network recognizing hand-written digits.

Images and labels in the MNIST database are in a binary format and gzipped. Several Shell or Awk scripts are developed to convert MNIST to LNN-acceptable formats (Appendix 4).

• bimg2vec: Convert MNIST image data to LNN-acceptable vectors
• blab2vec: Convert MNIST label data to LNN-acceptable vectors with one-hot encoding
• vec2lab: Convert LNN output vectors to text labels (the index of the maximal component)
• labdiff: Compare two text label files and print the accuracy

The original training and test image data are renamed to train.bimg.gz and test.bimg.gz respectively in this chapter. The regarding original label data are renamed to train.blab.gz and test.blab.gz.

The following commands generate several files for LNN.

$ gzip -d <train.bimg.gz | bimg2vec >train.in
$ gzip -d <train.blab.gz | blab2vec >train.out
$ paste train.in train.out >train.sam
$ gzip -d <test.bimg.gz | bimg2vec >test.in
$ gzip -d <test.blab.gz | blab2vec | vec2lab >test.lab

Some of these generated files are intermediate. The actually useful ones are the following.

• train.sam: LNN sample file for training
• test.in: LNN input file for test
• test.lab: Labels regarding to test.in

The structure of the network is x784i16s10m. It means the network uses cross entropy as the loss function. The network has a 784-dimension input layer, a 16-dimension hidden layer with the sigmoid activation function, and a 10-dimension output layer with the softmax activation function. The output is regarded as the probability distribution of which digit the image is. The image will be labeled by the maximal component of the output.

The network is trained using the following command.

$ lnn train -C x784i16s10m -r3 -b64 -i4096 <train.sam >model.nn

The network is trained for 4096 iterations. The -r option sets the learning rate to 3. The -b option sets the batch size to 64.

The following command runs the model on the test set and the output vectors are converted to labels.

$ lnn run -m model.nn <test.in | vec2lab >out.lab

The first several output labels are checked and compared with the test set by the following command.

$ paste out.lab test.lab | head
7       7
2       2
1       1
0       0
4       4
1       1
4       4
9       9
5       5
9       9

The following command shows that the accuracy is 93.71%.

$ labdiff out.lab test.lab
0.9371

4. Recognizing Spam SMS Texts

The SMS Spam Collection [1] is a public set of SMS labeled messages that have been collected for mobile phone spam research. This chapter uses this data set to train a network recognizing SMS spams.

The data set is a text file, renamed sms.txt in this chapter. Each line of sms.txt contains a message and its label, separated by a tab character. The label ham represents the message is a regular message. The label spam represents the message is a spam. The following snippet demonstrates the format of sms.txt.

ham     Oh k...i'm watching here:)
spam    Call FREEPHONE 0800 542 0578 now!

The 256 top frequent words from spam messages and regular messages are selected respectively. These 512 words are combined and duplicated ones are deleted. 408 unique words are left. The following shows some of them.

texts   sorry
finish  claim
ill     why
at      player
after   too

Each message is encoded to a 408-dimension vector. The component of a vector is the frequency (rate) of the word. The label is encoded to 1 if the message is a spam, otherwise 0.

Data are divided into a training set with 4763 regular messages and 683 spam messages and a test set with 64 regular messages and 64 spam messages. The training set and the test set are named train.sam and test.sam respectively.

The code of the above preprocess is documented in Appendix 5.

A b408i1s network is trained. This network uses the binary cross entropy as the loss function and contains a 408-dimension input layer, 1-dimension output layer, no hidden layer. The output is regarded as the probability of the message to be a spam. The input is regarded as a spam if the output is greater than 50%.

The network is trained for 64 epoches. Each epoch contains 128 iterations with the batch size to be 1024. The learning rate of each epoch is \(200(1-a)\), where \(a\) is the current accuracy. The model with maximal accuracy among epoches is selected.

#!/bin/bash

set -e
t=$(mktemp /tmp/lnn.spam.XXXXXX)
lnn train -C b408i1s </dev/null >$t
acc=0
max=0
for ((i=0;i<64;i++)); do
        lr=$(echo "(1-$acc)*200" | bc -l)
        lnn train -i128 -b1024 -r$lr -m $t <train.sam >$t.swp
        mv $t.swp $t
        acc=$(
                paste \
                        <(
                                <test.sam awk '{$NF=""}1' |
                                lnn run -m $t |
                                awk '{print ($0>0.5?1:0)}'
                        ) \
                        <(awk '{print $NF}' test.sam) |
                awk '$1==$2{e++}{n++}END{print e/n}'
        )
        echo $i $acc
        if [ $(echo "$acc > $max" | bc -l) -eq 1 ]; then
                max=$acc
                cp $t model.nn
        fi
done
echo $max
rm $t

This training script uses non-POSIX features, thus the shebang comment is #!/bin/bash instead of #!/bin/sh.

The following figure shows the result selected from many experiments. The maximal accuracy is 94.53%.

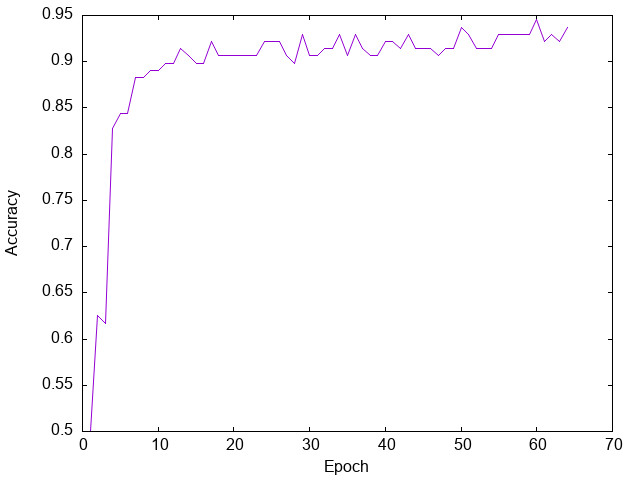
Figure 1.

5. Remarks

LNN attempts to make easy tasks esily done. It provides cross-language simple interfaces. This could decrease the cost of learning the utility. Users could call LNN with any programming language as long as the language could call external processes.

However, LNN is limited by the inter-process communication (IPC) mechanism of the operating system. UNIX-compatible systems use texts or byte streams for IPC. This makes it hard to pass executable code to LNN. Thus comparing to traditional deep learning frameworks, it is less flexible. Users can’t set customized activation functions or loss functions.

One possible way to support customized functions, is passing program names and arguments to LNN. LNN then calls the specified program and communicate with it by IPC. However, this approach requires a protocol about how the external program reads and prints. Activation and loss functions are usually very simple. Thus the main cost of writing these functions would be parsing and formatting. This will break the main target of LNN: easy tasks easily done. If a task requires customized activation or loss functions, a traditional deep learning framework may be a better choice.

Appendix 1. Training Options

Syntax	Description	Default
-C STR	Create a new model with the specific structure
-m FILE	Specify an existed model
-R NUM	Set the parameter of the L2 regularization
-i NUM	Set the number of iterations	32
-r NUM	Set the learning rate	1
-b NUM	Set the batch size

Table 1.

Appendix 2. Loss Functions

This appendix assumes the network has \(D\)-dimension output. The \(i\)-th component of the output vector is denoted by \(y_i\). The \(i\)-th component of the target vector is denoted by \(t_i\).

Character	Description	Formula
q	Quadratic error	\[ \frac{1}{2}\sum_{i=1}^{D}{(y_i-t_i)^2} \]
b	Binary cross entropy	\[-\sum_{i=1}^{D}{(t_i\log{y_i} + (1-t_i)\log{(1-y_i)})} \]
x	Cross entropy	\[ -\sum_{i=1}^{D}{t_i\log{y_i}} \]

Table 2.

Appendix 3. Activation Functions

This appendix assumes the dimension of the layer is \(D\). The weighted input value to the \(i\)-th neuron of the layer is denoted by \(x_i\). The output value of the \(i\)-th neuron of the layer is denoted by \(y_i\).

Character	Description	Formula
i	Identity	\[ y_i = x_i \]
s	Sigmoid	\[ y_i = \frac{1}{1+e^{-x_i}} \]
t	Tanh	\[ y_i = \frac{e^{x_i} - e^{-x_i}}{e^{x_i} + e^{-x_i}} \]
r	ReLU	\[ y_i=\left\{ \begin{align} &x_i, &x_i \gt 0\\ &0, &otherwise \end{align} \right. \]
m	Softmax	\[ y_i=\frac{e^{x_i}}{\sum_{k=1}^{D}{e^{x_k}}} \]

Table 3.

Appendix 4. MNIST Utilities

bimg2vec

#!/bin/sh

set -e

xxd -p -c1 -g1 |
awk '
        { $0 = sprintf("%d", "0x"$0) }
        NR <= 8 { next }
        NR <= 12 { h = h*256 + $0; next }
        NR <= 16 { w = w*256 + $0; next }
        NR == 17 { c = w*h }
        {
                printf "%f", $0/255
                if (++i == c) {
                        printf "\n"
                        i = 0
                } else
                        printf " "
        }
'

blab2vec

#!/bin/sh

set -e

xxd -p -c1 -g1 |
awk '
        { $0 = sprintf("%d", "0x"$0) }
        NR < 9 { next }
        {
                for (i = 0; i < 10; i++) {
                        if (i > 0)
                                printf " "
                        printf "%d", (i == $0 ? 1 : 0)
                }
                print ""
        }
'

vec2lab

#!/usr/bin/awk -f

{
        max = 1;
        for (i = 1; i <= NF; i++)
                if ($i > $max)
                        max = i;
        print max - 1
}

labdiff

#!/bin/sh

paste "$1" "$2" | awk '
        { n++ }
        $1 == $2 { c++ }
        END { print c/n }
        
'

Appendix 5. SMS Spam Utilities

#!/bin/sh

set -e
d=`mktemp -d /tmp/lnn.sms.XXXXXX`

topfreq()
{
        awk '
        {
                for (i=1; i<=NF; i++)
                        freq[$i]++;
        }
        END {
                for (word in freq)
                        if (word ~ /^([a-z]|\.|\?|!|'\'')+$/)
                                print word, freq[word]
        }
        ' "$@" | sort -rnk2,2 | head -n 256 | cut -d' ' -f1
}

txt2vec()
{
        awk -v lab="$1" -vd=$d '
        BEGIN {
                wtab=d"/wtab.txt"
                while (getline <wtab)
                        wd[$0] = d++
        }
        {
                for (i=1; i<=d; i++)
                        v[i] = 0
                for (i=1; i<=NF; i++)
                        if ($i in wd)
                                v[wd[$i]] += 1/NF
                for (i=0; i<d; i++) {
                        if (i > 0)
                                printf " "
                        printf "%f", v[i]
                }
                if (length(lab) > 0)
                        print " "lab
                else
                        print ""
        }
        '
}

(
        awk -F '\t' '$1=="spam"{print $2}' sms.txt | topfreq
        awk -F '\t' '$1=="ham"{print $2}' sms.txt | topfreq
) | sort | uniq >$d/wtab.txt
awk -F '\t' -v d=$d '
        $1 == "spam" {
                if (spam++ < 64)
                        file=d"/spam-test.txt"
                else
                        file=d"/spam-train.txt"
        }
        $1 == "ham" {
                if (ham++ < 64)
                        file=d"/ham-test.txt"
                else
                        file=d"/ham-train.txt"
        }
        {
                print $2 >file
        }
' sms.txt
(txt2vec 1 <$d/spam-train.txt && txt2vec 0 <$d/ham-train.txt) \
        >train.sam
(txt2vec 1 <$d/spam-test.txt && txt2vec 0 <$d/ham-test.txt) \
        >test.sam
wc -l $d/wtab.txt
rm -r $d

References